Atómové jadra sú objekty mikrosveta, ktorý sa riadi pravidlami kvantovej teórie. Pod pojmom „spin“ je v kvantovej teórií označovaný vnútorný rotačný moment objektov mikrosveta. Je to čisto kvantovomechanický efekt, ktorý nemá obdobu v klasickej mechanike. Jeho klasickou analógiou je rotačný moment telies rotujúcich okolo vlastnej osi rotácie.
Spin je podobne ako klasický rotačný moment telies vektorová veličina (označenie I ) s rovnakým rozmerom základnej jednotky (Joule.s). Pre praktické dôvody sa však veľkosť spinu atómových a subatómových objektov vyjadruje v jednotkách ħ (redukovaná Planckova konštanta, ħ = 1,054571817 . 10-34 Joule.s). Podľa kvantovej teórie je veľkosť spinu kvantovaná a je charakterizovaná spinovým kvantovým číslom I. I môže nadobúdať iba nezáporné celé alebo poloceločíselné hodnoty: I = 0, 1/2, 1, 3/2,… . Veľkosť vektora spinu je potom podľa kvantovej teórie daná výrazom:
\qquad\qquad\qquad\qquad\qquad I=\hbar \sqrt{I.(I+1)}\qquad \qquad\qquad\qquad\qquad\qquad\qquad(1)Spin atómových jadier je odvodený od spinu neutrónov a protónov. Ich spin je zasa odvodený od spinu kvarkov, z ktorých sa tieto nukleóny skladajú. K celkovému spinu nukleónov prispieva okrem vlastného spinu kvarkov aj ich orbitálny moment hybnosti. Presný mechanizmus vzniku výsledného spinu nukleónov je zložitý a zatiaľ nie je jednoznačne potvrdený (resp. teória je veľmi komplikovaná [Proton spin crisis – Wikipedia] ). Empiricky však bolo potvrdené, že oba nukleóny protón i neutrón majú spin I = 1/2.
Mechanizmus skladania spinov nukleónov v atómových jadrách je taktiež zložitý, no pre celkový spin jadier sú známe tieto jednoduché pravidla:
- Jadrá s párnym počtom protónov i neutrónov majú nulový spin (I = 0). Patria sem napr. jadrá izotopov 12C, 16O. Tieto jadrá nevykazujú NMR jav.
- Jadrá s nepárnym počtom nukleónov (suma protónov a neutrónov v jadre) majú poloceločíselný spin (I = 1/2, 3/2, 5/2…).
- Jadrá s nepárnym počtom protónov i nepárnym neutrónov majú spin celočíselný (I = 1, 2, 3,…).
Jadrá s nenulovým spinom, teda jadrá ktoré sú NMR aktívne je v NMR terminológií zvykom označovať zjednodušene ako „spiny“.
Z kvantovej teórie ako aj zo Stern-Gerlachovho experimentu [Stern–Gerlach experiment – Wikipedia] vyplýva, že nie iba celková veľkosť spinu ale aj veľkosť jeho zložiek (Ix, Iy a Iz) je kvantovaná, pričom veľkosť zložiek vektora spinu sa dá vyjadriť ako súčin redukovanej Planckovej konštanty ħ a kvantového čísla m (napr. Ix = m.ħ). Číslo m sa nazýva magnetické kvantové číslo. V závislosti od veľkosti čísla I magnetické kvantové číslo m môže nadobúdať iba 2I+1 diskrétnych hodnôt :
m ∈ {-I, –(I-1),–(I-2) ……. +(I-2),+(I-1),+I }.
Pre organickú chémiu a biochémiu sú najdôležitejšie jadrá so spinom I = 1/2 (patria sem napr. jadrá izotopov 1H, 13C, 15N, 31P). Pre tieto jadrá m môže nadobúdať iba 2 hodnoty: m =+1/2 a m =-1/2. Dôsledkom tohto kvantovania je, že všetky merateľné veličiny, ktoré charakterizujú stav spinov I = 1/2 ( energia, zložky vektora spinu) môžu nadobúdať iba 2 dovolené hodnoty. Vo všeobecnosti nie je determinované ktorú hodnotu z 2 možných pri meraní skutočne určíme. Známa je iba štatistická pravdepodobnosť s akou jednotlivé hodnoty nameriame.
Čo sa týka energie pre spiny I = 1/2 existujú iba 2 stavy, v ktorých je dobre definovaná. Tieto stavy je zvykom formálne označovať ako |α> a |β>. V stave |α> je energia spinu rovná (vyjadrená v rad/s) Eα = –½ γB0 a v stave |β> je rovná Eβ = +½ γB0 , kde konštanta γ je tzv. gyromagnetický pomer (pozri v nasledujúcom odseku).
Vo všeobecnosti sú spiny I = 1/2 v zmiešanom stave |ψ> danom ako superpozícia stavov |α> a |β> :
|ψ>=cα|α> + cβ|β>.
Koeficienty (komplexné čísla) cα a cβ určujú podiel stavov |α> a |β> v zmiešanom stave a zároveň umožňujú určiť pravdepodobnosť namerania jednotlivých dovolených hodnôt energie. Pravdepodobnosť že nameriame hodnotu Eα alebo Eβ je rovná p(Eα)=cα2, resp. p(Eβ) = cβ2. Platí pritom, že vždy nameriame jednu z týchto 2 možnosti, čiže: p(Eα)+p(Eβ) = cα2 + cβ2= 1
Keďže (ako uvidíme neskôr) energia spinu súvisí s hodnotou Iz zložky spinu, v stave s dobré definovanou energiu spinu sú dobre definované aj z-zložky vektora spinu: Iz(α)= +1/2ħ a Iz(β)=-1/2ħ .
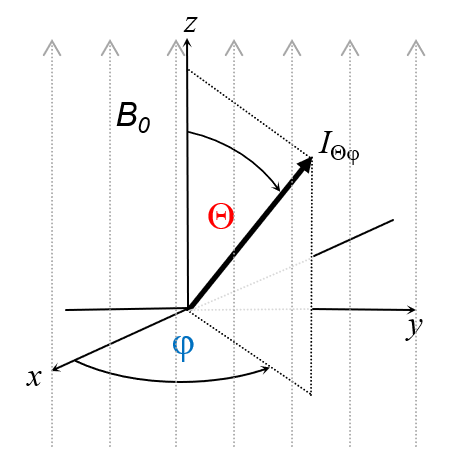
Z kvantovania veľkosti zložiek vektora spinu vyplýva, že vektor spinu má veľmi zvláštne vlastnosti. Na rozdiel od vektora klasického momentu hybnosti vektor spinu nemá dobre definovanú orientáciu v priestore: miesto 3 ortogonálnych (nezávislých) zložiek potrebných na jej jednoznačne určenie (napr. zložiek Ix, Iy a Iz), má dobre definovanú iba jednu z nich. V závislosti od stavu spinu má táto dobre definovaná zložka rôznu orientáciu v priestore. Táto dobre definovaná zložka sa zvykne označovať ako „Blochov vektor“ [Bloch Sphere – Wikipedia, the free encyclopedia]. Smer, v ktorom je Blochov vektor orientovaný sa obvykle vyjadruje v polárnych súradniciach Θ a φ (pozri obr.2.). Pri tomto vyjadrení súradníc stav Blochovho vektora |ψ> možno vyjadriť ako superpozíciu stavov |α> a |β>, pričom koeficienty cα a cβ sú určené súradnicami Θ a φ.:
|ψ>=cα|α> + cβ|β> = cos(Θ/2)|α>+ sin(Θ/2)eiφ|β>
Zložka spinu v smere danom súradnicami Θ a φ má vždy hodnotu IΘ,φ = +ħ/2. Ix, Iy a Iz zložky vektora spinu pritom nie sú dobré definované. Pri ich opakovanom meraní sa náhodne namerajú hodnoty +ħ/2 alebo –ħ/2. Spriemerované hodnoty veľkého počtu týchto meraní (alebo spriemerované hodnoty veľkého súboru spinov, ktoré boli pred meraním v rovnakom stave) sú však dobre definované a dajú sa vyjadriť ako priemet Blochovho vektora do smeru osi x, y a z :
< Ix >= ½ħ.sinΘ cosφ, < Iy >= ½ħ.sinΘ sinφ a < Iz >= ½ħ.cosΘ
, kde < Ii > označuje kvantovomechanickú spriemernenú hodnotu zložky spinu Ii .
Vidíme, že spriemerované hodnoty zložiek Blochovho vektora sú definované podobným spôsobom ako zložky klasických vektorov. Pri NMR meriame vždy veľký súbor spinov a získavame informácie iba o spriemerovanom správaní spinov. V ďalšom (pokiaľ explicitne neuvedieme inač) budeme preto za vektor spinu považovať Blochov vektor IΘ,φ= ½ħ (sinΘ cosφ; sinΘ sinφ; cosΘ), ktorý má správanie podobne správaniu klasického vektora momentu hybnosti. Tento prístup nám zjednoduší popis mnohých NMR javov.