Spektrá 1. poriadku poskytujú spinové systémy zložené iba zo slabo interagujúcich spinov. Patria sem napríklad všetky spinové systémy uvedené v predchádzajúcom odstavci okrem systému AA’XX‘, ktorý obsahuje skupiny chemicky ekvivalentné spiny.
Spektrá 1. poriadku sa vyznačujú tým, že signály v nich obsiahnuté majú jednoduchú symetrickú štruktúru s dobre definovanými intenzitami spektrálnych čiar. Počet a intenzita spektrálnych čiar v multiplete spinu I, patriaceho do systému slabo interagujúcich spinov sa dá jednoducho odvodiť z diagramu jeho povolených energetických stavov (obr.44 ).
Pre izolovaný spin I existujú iba 2 stavy s dobre definovanou energiou (|α> a |β>). Koherencia, ktorá vznikne z týchto stavov má frekvenciu danú chemickým posunom νI. V dvojspinovom IM systéme každá energetická hladina spinu I zmení svoj stav v dôsledku interakcie so spinom M o hodnotu +JIM /4 alebo –JIM /4, v závislosti od znamienka interakčnej konštanty a stavu spinu M. Keďže oba stavy spinu M (|α> a |β>) sú rovnako pravdepodobne obe možnosti sa realizujú s rovnakou pravdepodobnosťou. Z pôvodnej hladiny vzniknú 2 nové so zmenenou energiou. Počet stavov s dobre definovanou energiou spinu I sa účinkom spinu M preto zdvojnásobí. Vznik nových stavov je príčinou, že po excitácii spinov môžu vzniknúť 2 rozdielne koherencie prislúchajúce spinu I: |αβ>↔|ββ> a |αα>↔|βα> (prvý symbol označuje stav spinu I, druhý stav spinu M). Vidíme, že v týchto koherenciách je aktívny (zmiešavanie stavov |α> a |β>) iba spin I. Druhý spin M svoj stav nemení (pasívny spin). Pretože populácia oboch stavov pasívnych spinov je prakticky rovnaká, intenzita oboch koherencií je rovnaká.
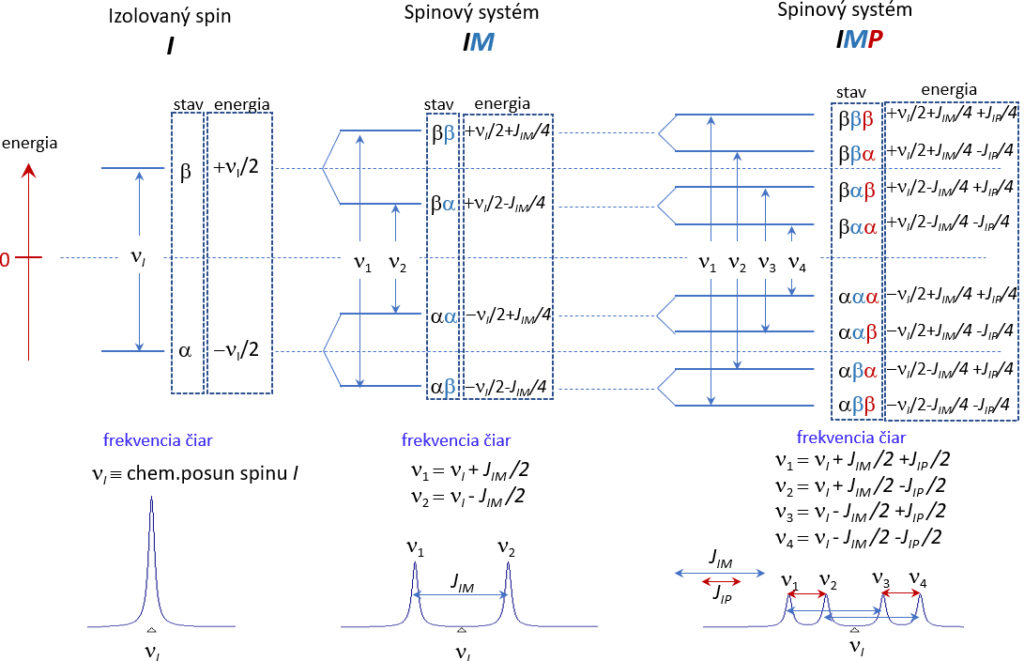
Pre väčšie spinové systémy slabo interagujúcich spinov spinovým číslom I=1/2 možno energetickú schému a tým aj multipletovú štruktúru aktívneho spinu určiť podobným spôsobom ako pre to je ukázane na obr. pre spin I v IMP systéme. Vychádza sa vždy z jednospinového systému (izolovaný spin I) a postupne sa pridáva interakcia pasívnych spinov. Každý ďalší pasívny spin zdvojnásobí počet možných stavov aktívneho spinu. Multiplet spinu I vytvárajú iba koherencie aktívneho spinu, v ktorých pasívne spiny zostávajú v nezmenenom stave. Pri n-pasívnych spinov má aktívny spin v multiplete 2n spektrálnych čiar. Jeho tvar sa dá vo všeobecnosti charakterizovať ako dublet dublet….dubletu (ddd..d). Multiplet je vždy symetrický okolo svojho stredu, ktorý leží na chemickom posune νI. Každá interakcia I s pasívnym spinom M,P,.. sa prejaví existenciou dvojice (dvojíc) spektrálnych čiar navzájom frekvenčne separovaných o hodnotu JIM,. JIP,… Samozrejme málokedy všetky čiary ddd..d multipletu je možne v spektre rozlíšiť. Hlavnou príčinou je nedostatočné rozlíšenie NMR signálov spôsobené relatívne malými rozdielmi v hodnote interakčných konštánt JIM,. JIP,. a nenulovou šírkou spektrálnych čiar. Ďalšou príčinou, nezávislou od rozlíšenia spektrálnych čiar, sú interakcie s magneticky ekvivalentnými spinmi. Rovnaká interakcia so všetkými členmi magneticky ekvivalentnej skupiny spinov spôsobí, že v energetickej schéme aktívneho spinu vzniknú viacnásobne degenerované hladiny (prislúchajúce súčasne viacerým stavom). Napr. ak by boli v 3-spinovom IMP systéme spiny MP ekvivalentné (IMP→ IM2, JIM,= JIP), potom by hladiny |ββα> a |βαβ> mali rovnakú energiu. Podobná rovnosť by platila aj pre hladiny |αβα> a |ααβ>. Dôsledkom by bolo, že koherencie |ββα>↔|αβα> a |βαβ>↔ |ααβ> by mali rovnakú frekvenciu (ν2=ν3) a v spektre by sa prekrývali, v dôsledku čoho by intenzita ich spoločnej spektrálnej čiary mala dvojnásobnú intenzitu. Multiplet by mal vzhľad tripletu s intenzitami 1:2:1.
Vo všeobecnosti skupina n ekvivalentných spinov štiepi všetky už existujúce spektrálne čiary spinu I (vzniknuté v dôsledku interakcie s inými spinmi, s ktorým je v interakcií) na n+1 čiarový multiplet s intenzitami čiar úmernými binomickým koeficientom: (ⁿ
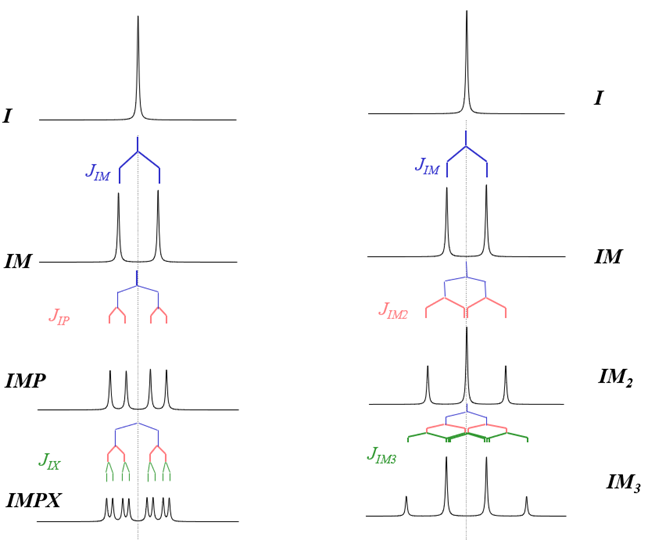
Aj keď je štruktúra multipletov 1.poriadku je veľmi jednoduchá ich vzhľad môže byť komplikovaný a ich analýza zložitá. Príčinou môže byť prekryv viacerých čiar a to v dôsledku existencie podobnosti (totožnosti) viacerých interakčných konštánt a nenulovej šírkou spektrálnych čiar.
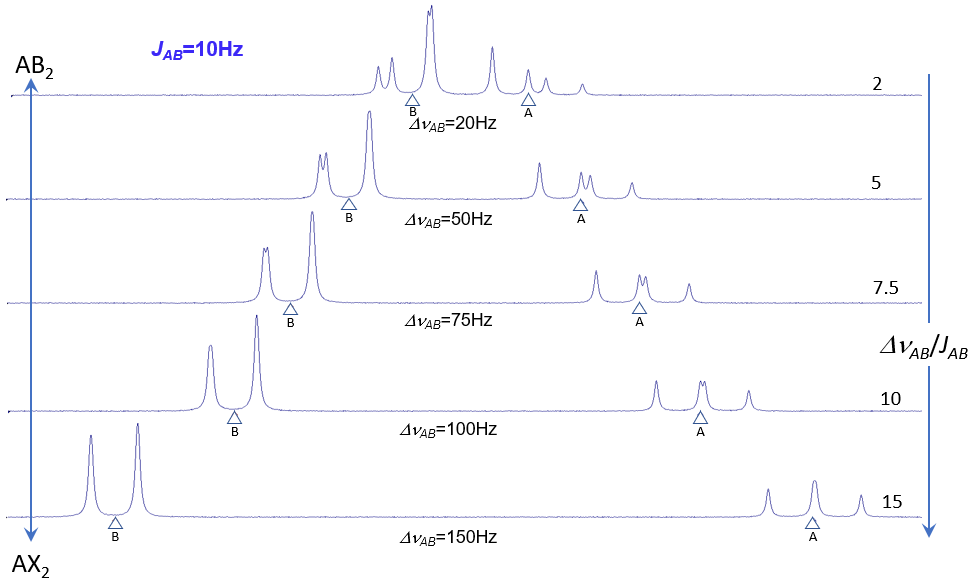
Podmienka slabej interakcie je striktne splnená iba pre heteronukleárne dvojice spinov, napr. pre 1H a 19F spiny v di-fluórmetáne. Pre homonukleárne 1H systémy interakcie medzi spinmi vždy spôsobujú odchýlku od ideálnych spektier 1.poriadku. Ak |∆νAX /JAX|>8-10 je to iba malá odchýlka v intenzite spektrálnych čiar od predpokladanej intenzity. Pre menšie hodnoty |∆νAX /JAX| sú odchýlky intenzít výraznejšie a v spektre sa začínajú objavovať ďalšie (kombinačné) čiary. Pri hodnote |∆νAX /JAX|~ 3, signály interagujúcich spinov strácajú podobnosť so signálmi slabo interagujúcich spinov a na ich analýzu je potrebne použiť formalizmus kvantovej mechaniky. Na obr. 46 je ukázaný efekt sily interakcie medzi neekvivalentnými spinmi v AB2 spinovom systéme. Vidíme, že pri hodnote |∆νAB /JAB|> 10 spektrum sa veľmi dobre podobá na predpokladané spektrum AX2 systému. Najviac viditeľnou odchýlkou je nerovnosť intenzít v dublete prislúchajúcemu X spinom. Podobnosť s AX2 typom spektra sa už úplne stráca pri hodnotách |∆vAX /JAX|~ 5.