Interakcie medzi magnetickými dipólmi spinov, ktoré sa prenášajú priamo cez priestor označujeme ako D- alebo DD-interakcie (od „direct“ alebo „dipól-dipól“ ). Na rozdiel od J-interakcií, pri ktorých je veľkosť interakcie medzi 2 spinmi v kvapalnej fáze vyjadrená jedným číslom (interakčnou konštantou), veľkosť D-interakcií má podstatne zložitejšiu závislosť od ich vzájomného priestorového usporiadania. Na obr.55 je uvedený vzťah pre energiu interakcie medzi dvojicou spinov mimo magnetického poľa.
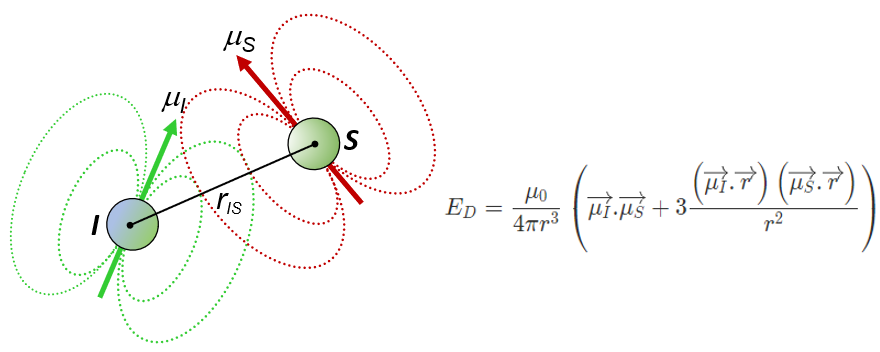
Pre dvojicu spinov umiestnenú v silnom magnetickom poli sa vzťah pre energiu zjednoduší lebo rýchla precesia spinov okolo B0 spriemerní orientácie spinov do smeru osi z. V poli B0 je orientačný člen závislý iba od orientácie vektora spojnice spinov r k B0. Zjednodušenie je väčšie pre heteronukleárnu dvojicu spinov (energia interakcie závisí iba od z– zložiek spinu) ako pre homonukleárny systém (energia závisí aj od x, y – zložiek spinu). Kvantovo mechanické vyjadrenie energie dipólovej interakcie dvojicu spinov (Hamiltonián) v silnom magnetickom poli je:
H_{D}= d_{IS}\left( 1-3cos^{2}\theta \right)\left[ I_{z}S_{z}-\color{Red} 1/2(I_{x}S_{x}+I_{y}S_{y}) \color{Black} \right], kde\\
d_{IS}=\frac{\mu_{0}\gamma_{I}\gamma_{S}\hbar ^{2}}{4\pi (r_{IS})^{3}}
,kde červenou farbou uvedené členy je potrebné uvažovať iba pre homonukleárne dvojice spinov.
Uhol θ (0° až 180) je uhol medzi spojnicou spinov I a S a poľom B0. Orientačný člen (1-3cos2θ) môže nadobúdať hodnoty v rozsahu -2 (pre θ = 0° alebo 180°) až +1 (pre θ = 90°). Pri θ = 54,74° (tzv. magický uhol) sa orientačný člen rovná nule. dIS = (μ0γIγSħ2)/4πr3IS sa nazýva dipól-dipólová interakčná konštanta pričom μ0 je permeabilita vákua (4π.10-7 kg.m.s-2.A-2), rIS je vzdialenosť medzi spinmi, γI a γS sú gyromagnetické pomery spinov I a S.
Z Hamiltoniánu vyplýva, že DD interakcia pre heteronukleárny IS systém sa formálne podobá na slabú J-interakciu spinov, pričom veľkosť interakcie (miesto konštanty J) vyjadruje výraz dIS (1- cos2θ ). V spektre oboch spinov sa preto DD interakcia prejaví ako symetrický dublet s veľkosťou štiepenia DIS = dIS (1- cos2θ ).
Ako bolo povedané vyššie, pre silne interagujúcu dvojicu spinov rovnakého druhu, je potrebné do Hamiltoniánu zahrnúť aj členy s x, y– zložkami spinov. To má dva efekty: prvý, že DD interakcia sa (na rozdiel od J-interakcie) v spektre prejaví aj pre ekvivalentné spiny a druhý efekt, že veľkosť štiepenia v dublete je o 50% väčšia ako pre heterenukleárnu dvojicu spinov, čiže pre dvojicu spinov rovnakého druhu platí DIS = 3/2dIS (1- cos2θ ).
Z výrazu pre DIS vidíme, že veľkosť dIS číselne zodpovedá štiepeniu dubletu pre dvojicu spinov so spojnicou orientovanou kolmo na B0 (θ = 90). Vidíme tiež že dIS veľmi rýchle klesá so zväčšovaním vzdialenosti rIS medzi spinmi I a S. V nasledujúcej tabuľke sú uvedené hodnoty dIS pre vzdialenosti medzi atómami, ktoré sú v bežných molekulách (vyjadrené v angströmov; 1Å=10-10 m).
| rIS [Å] | dHH [Hz] | dHC [Hz] | dHN [Hz] |
| 1 | 120 000 | 30 000 | 12 000 |
| 2 | 15 000 | 3 750 | 1 500 |
| 3 | 4 444 | 1 111 | 444 |
| 4 | 1 875 | 469 | 188 |
| 5 | 960 | 240 | 96 |
| 10 | 120 | 30 | 12 |
| 20 | 15 | 2 | 1,5 |
| 30 | 4,4 | 1,1 | 0,4 |
| 40 | 2 | 0,5 | 0,2 |
Pre praktickú ilustráciu sú v nasledujúcom obrázku uvedené hodnoty rIS a dIS pre dvojice spinov v zabrzdenej stoličkovej konformácií molekuly cyklohexánu.

Na záver tejto časti je potrebné zdôrazniť jednu významnú vlastnosť DD interakcií. Keďže DD interakcie závisia od orientácie spojnice medzi interagujúcimi spinmi k poľu B0, umožňujú porovnávať orientáciu spinov aj vo vzdialených fragmentov molekúl. Hovoríme, že DD interakcie majú potenciál poskytovať aj štruktúrne informácie „ďalekého dosahu“ (long-range).







