Magnetický moment je prostriedkom pomocou ktorého spiny interagujú s okolím. Magnetický moment interaguje s magnetickými poľami, v ktorých sa nachádza. Môžu to byť polia externé ale aj polia interné pochádzajúce zo vzorky.
Najskôr vyšetrime správanie spinov vo vonkajšom statickom magnetickom poli v akom sa NMR experiment vždy vykonáva. Označme toto pole symbolom B0 a smer jeho siločiar za smer z-osi laboratórnej súradnicovej sústavy (LSS).
Na spiny mimo magnetického poľa nepôsobí žiadna sila, a preto spiny zostávajú v rovnakom stave a nemení sa ich poloha ani orientácia. Orientačná (polohová) energia pre všetky spiny v nulovom poli nezávisle od ich orientácie je rovnaká – nulová: Eθ,φ = 0 pre všetky hodnoty Θ a φ ak B0 = 0.
Naopak, v nenulovom poli sa stav spinov mení. Nie sú to však zmeny medzi č
istým stavom |α> a |β> ako sa to v literatúre často interpretuje, ale sú to periodické zmeny zmiešaného stavu spinov. Adekvátny popis je iba kvatovomechanický popis (tzv. časovo závislá Schrodingerova rovnica). Ak však “kvantový” vektor spinu nahradíme Blochovým vektorom možno použiť jednoduvhý klasický popis, čo aj v nasledujúcom využijeme.
V nenulovom magnetickom poli B0 potenciálna energia závisí od vzájomnej orientácie vektorov magnetickej indukcie a magnetického momentu spinu. Je daná skalárnym súčinom vektorov μ a B0, kde μ je magnetický moment spinu odvodený od Blochovho vektora:
EΘ,φ= –μ.B0 =-μz.B0= –μ.B0.cos(Θ)=-½ħ.γB0.cos(Θ)=-½ħ.ω0.cos(Θ).
,kde ω0=γ.B0 má rozmer frekvencie [rad/s]. Vidíme, že energia spinu závisí od uhla Θ medzi vektormi μ a B0 . Najmenšiu hodnotu potenciálnej energie má magnetický moment ak je orientovaný v smere B0 (Θ = 0°) . Najväčšiu energiu má spin ak je orientovaný proti smeru B0 (Θ = 180°). Dôležité je, že energia spinov nezávisí od uhla φ, t.j. od ich orientácie v rovine x,y.
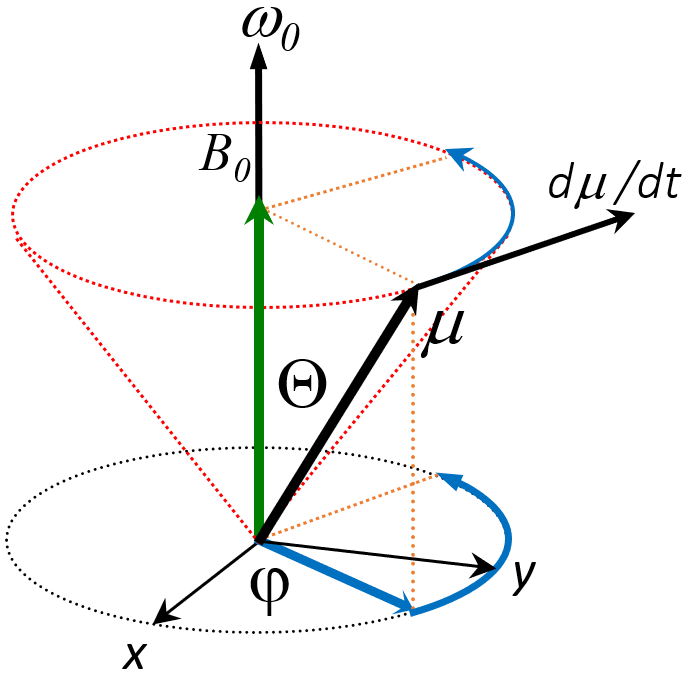
Ak by spin jadra bol nulový a napriek tomu by jadro malo nenulový magnetický moment μ, potom by sila úmerná gradientu potenciálnej energie (FΘ = –grad (μ.B0)) spôsobila by zmenu jeho orientácie do smeru B0, tak ako je to v prípade magnetky kompasu. Existencia spinu však spôsobí, táto sila pôsobila na spinI momentom sily T = μ x B0 a že spin začne precesovať okolo smeru magnetického poľa. Precesia je výsledkom točivého momentu sily T, ktorým B0 pôsobí na μ. Výsledkom je zmena orientácie I, a teda aj μ. Podľa klasickej mechaniky opis pohybu I (účinok točivého momentu T) vyjadruje vektorová diferenciálna rovnica:
\frac{d(\gamma I)}{dt}=\frac{d \mu}{dt}=\gamma(\mu\times B_{0})=\mu\times \gamma B_{0}=\mu\times \omega_{0} \tag{1a}
,kde μ je magnetický moment odvodený od Blochovho vektora I. Na riešenie tejto vektorovej rovnice je vhodne oba vektory vyjadriť pomocou ich x, y a z zložiek: μ ≡ ½ħγ(sinΘcosφ; sinΘsinφ; cosΘ) a podobne B0 ≡ (0; 0; B0). Rozpísaním vyššie uvedenej vektorovej rovnice na jej zložky dostaneme 3 skalárne rovnice:
\frac{d\mu_{x}}{dt}=\mu_{y}.\omega_{0}; \space \space \space \space \frac{d\mu_{y}}{dt}=-\mu_{x}.\omega_{0}; \space \space \space \space \frac{d\mu_{z}}{dt}=0 \tag{1b}
Ak urobíme 2.deriváciu týchto zložiek dostaneme diferenciálne rovnice 2.stupňa (napr. d2μx/dt2 = –(ω0)2.μx ), ktorých riešením (pri konštantnom ω0 ) sú 3 integrálne rovnice pre jednotlivé zložky vektora μ:
μx(t) = ½ħγsin(Θ).cos(φ+ω0t), μy(t) = ½ħγ.sin(Θ).sin(φ+ω0t), μz(t) = ½ħγ.cos(Θ),
kde φ je počiatočná fáza μ. Vidíme, že spin (jeho dobre definovaná zložka, Blochov vektor) vykonáva precesný pohyb okolo vonkajšieho poľa, ktoré na spin pôsobí. V polárnej súradnicovej sústave sa dá pohyb jednoducho popísať:
- Pri precesií sa polárny uhol Θ (odchýlka μ od smeru B0 ) nemení, nemení sa preto ani polohová energia spinu a ani hodnota jeho zložky μz.
- Fáza (orientácia μ v rovine xy) sa rovnomerne mení s časom s uhlovou rýchlosťou ω0 [rad.s-1] úmernou indukcií B0.
- Z predchádzajúceho vyplýva, že vzájomná orientácia rôznych spinov toho istého druhu a ich celková energia sa pri precesií taktiež nemenia.
Frekvencia precesie spinov ω0 sa označuje sa ako „Larmorova frekvencia“ . Často sa vyjadruje aj v Hz: ν0 = ω0/2π [Hz≡ s-1]. V závislosti od indukcie magnetického poľa, ktoré sú v súčasnosti pre pozorovanie NMR javu dostupné ( do 25Tesla) je hodnota Larmorovej frekvencie z oblasti rádiofrekvenčného pásma (kHz až ~ 1 GHz). Znamená to, že NMR prístroje sú rádiofrekvenčné aparatúry.
Okrem poľa B0 na spiny pôsobia aj interné (vnútro vzorkové) magnetické polia a môžu pôsobiť tiež ďalšie vonkajšie polia. Pohyb spinu v takomto prípade určuje výsledné (časovo premenlivé) magnetické pole B (t), ktoré je vektorovým súčtom všetkých poli pôsobiacich v danom okamžiku na spin. Okamžitá zmena stavu spinu sa dá potom naďalej vyjadriť vo forme rovnice (1), treba len zameniť B0 za B (t) a ω0 za ω(t) .
Pohybové rovnice zložiek spinu uvedené vyššie boli odvodené metódami klasickej teórie. Ako bolo uvedené v kapitole kvantová teória poskytuje pre pohyb spinov identické výsledky.
