1.6.6 DD – relaxácia

Najdôležitejší efekt DD-interakcií pre NMR v kvapalnej fáze súvisí s ich fundamentálnou úlohou pri relaxácií ¹H a ¹³C spinov. DD-interakcie sú totiž pre tieto spiny v diamagnetických molekulách dominantným spôsobom výmeny energie medzi spinmi navzájom ako aj výmeny energie s inými zdrojmi náhodných magnetických poli, čiže dominantným spôsobom ich NMR relaxácie.  Bez tohto relaxačného mechanizmu by NMR organických látok zďaleka nebola rutinná záležitosť. Navyše s DD-relaxáciou je spojený Nukleárny Overhauserov efekt (NOE), ktorý je zdrojom veľmi cenných štruktúrnych informácií.

Špecifičnosť DD-relaxácie je že ustaľovanie rovnovážnej populácie stavov spinov sa dosahuje nie iba „povolenými“  jednokvantovými spektrálnymi prechodmi individuálnych spinov ale aj prostredníctvom „zakázaných“ viackvantových spektrálnych prechodov skupiny spinov. Príčinou je existencia silnej väzby medzi spinmi v dôsledku ich vzájomnej DD-interakcie.

Základné črty DD-relaxácie si ilustrujeme na systéme dvoch priestorovo blízkych spinov I a S nachádzajúcich sa v jednej molekule. Existencia J-interakcie medzi týmito spinmi má zanedbateľný vplyv na efekt DD-relaxácie preto ju pri popise DD relaxácie budeme považovať za nulovú. Časovo spriemernený a teda konštantný Hamiltonian H₀ takéhoto systému potom obsahuje iba dva členy vyjadrujúce Zeemanov term (interakciu s poľom B₀) korigovaný chemickým posunom spinov: H₀ = ω_II_z+ω_sS_z , kde ω_i = γ_i B₀(1– σ_i) je absolútna frekvencia spinu i.  Časovo spriemernená DD-interakcia medzi spinmi I a S má nulovú hodnotu, a preto DD-interakcia k  H₀ neprispieva.

Hamiltonian H₀ má 4 stavy s dobre definovanou energiou. Sú to zjednotené stavy dané jednoduchou kombináciou dvoch základných stavov spinu I a spinu S |α> a |β>:

|α> + |α> → |αα> E_αα = E_α (I) + E_α(S)
|α> + |β> → |αβ> E_αβ = E_α(I) – E_β(S)
|β> + |α> → |βα> E_βα = –E_β(I) + E_α(S)
|β> + |β> → |ββ> E_ββ = –E_β(I) – E_β(S)

V zjednotenom stave |ij> prvý index indikuje stav spinu I, druhý index stav spinu S.

DD-interakcia medzi spinmi I a S sa prejaví ako porucha k Hamiltoniánu H₀. Tejto poruche zodpovedá časovo premenlivý Hamiltonian H_D(t).   Celkový, časovo premenlivý Hamiltonián H_t(t) je zložený z H₀ a H_D(t):  H_t(t)= H₀ +H_D(t).

Pretože veľkosť H_D(t) je rádovo menšia ako veľkosť H₀ možno efekt H_D(t) na vývoj spinového systému vyjadriť pomocou časovo závislej poruchovej teórie (time dependent perturbation theory). Táto teória postuluje, že porucha nemení bázické stavové funkcie a vlastné hodnoty energie Hamiltonianu H₀ ale iba generuje spektrálne prechody medzi stavmi H₀, ktoré majú dobre definovanú energiu. Schéma DD relaxačných ciest IS systému s vyznačením dovolených energetických stavov, možných spektrálnych prechodov medzi nimi ako aj ich frekvencií a pravdepodobnosti je ukázaná na nasledujúcom obrázku.

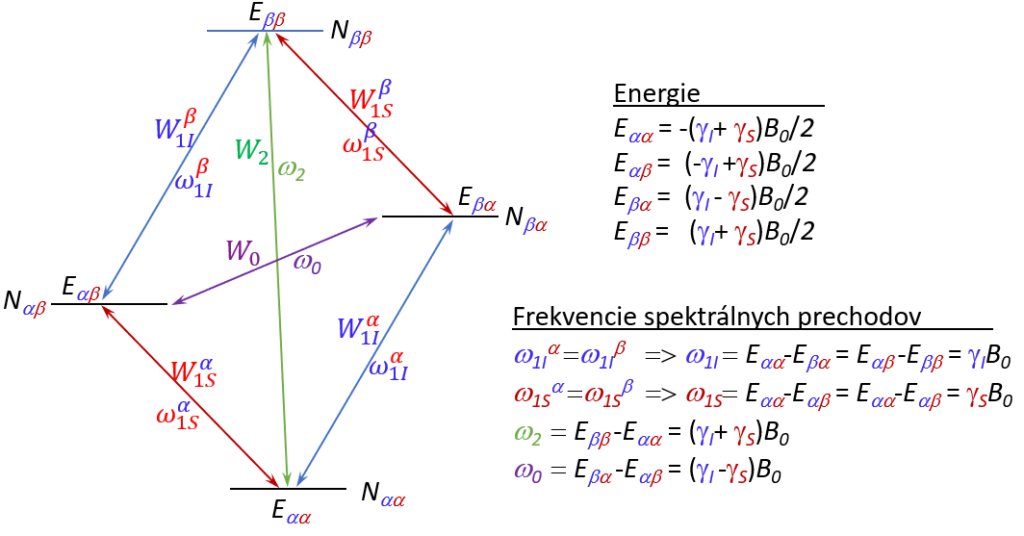
Pri odvodení vzťahov pre DD-relaxáciu budeme postupovať analogicky ako v odseku 1.6.2 pri popise M_z relaxácie jednospinového systému. Okamžitú z-zložku spinu I (I_z) a spinu S (S_z) možno vyjadriť ako rozdiel okamžitých populácií stavov spojených s dvomi spektrálnymi prechodmi spinu I resp. spinu S: Podobne možno vyjadriť aj rovnovážne zložky z-magnetizácie (označenie I⁰_z a S⁰_z):

\tiny{  I_z\sim\left(N_{\alpha\alpha}-N_{\beta\alpha}\right)+\left(N_{\alpha\beta}-N_{\beta\beta}\right)\ podobne{\ I}_z^0\sim\left(N_{\alpha\alpha}^0-N_{\beta\alpha}^0\right)+\left(N_{\alpha\beta}^0-N_{\beta\beta}^0\right)}\\

\tiny{S_z\sim\left(N_{\alpha\alpha}-N_{\alpha\beta}\right)+\left(N_{\beta\alpha}-N_{\beta\beta}\right)\ podobne\ S_z^0\sim\left(N_{\alpha\alpha}^0-N_{\alpha\beta}^0\right)+\left(N_{\beta\alpha}^0-N_{\beta\beta}^0\right)}

Časovú zmenu z-zložky magnetizácie spinu I ako aj spinu S možno vyjadriť rovnicami:

\tiny{dI_z/dt=d\left[\left(N_{\alpha\alpha}-N_{\beta\alpha}\right)+\left(N_{\alpha\beta}-N_{\beta\beta}\right)\right]/dt = dN_{\alpha\alpha}/dt-dN_{\beta\alpha}/dt+dN_{\alpha\beta}/dt-dN_{\beta\beta}/dt}\\ 
\tiny{dS_z/dt=d\left[\left(N_{\alpha\alpha}-N_{\alpha\beta}\right)+\left(N_{\beta\alpha}-N_{\beta\beta}\right)\right]/dt = dN_{\alpha\alpha}/dt-dN_{\alpha\beta}/dt+dN_{\beta\alpha}/dt-dN_{\beta\beta}/dt }

Populácie jednotlivých stavov sa budú meniť v dôsledku spektrálnych prechodov z iných stavov ako je to naznačené v schéme. Tak napr. hodnota N_αα sa bude zvyšovať 3 spektrálnymi prechodmi zo stavu |αβ>, |βα> a |ββ> na stav |αα> a naopak znižovať prechodmi zo stavu |αα> na stavy |αβ>, |βα> a |ββ>. Pravdepodobnosť jednotlivých prechodov v oboch smeroch je rovnaká a daná konštantami W_1S , W_1I a W_2IS .

Hnacou silou relaxácie sú odchýlky okamžitej populácie jednotlivých stavov od ich rovnovážnej hodnoty. Pre časovú zmenu N_αα možno preto vyjadriť nasledujúcou diferenciálnou rovnicou:

\tiny{dN_{\alpha\alpha}/dt=W_{1I}(N_{\beta\alpha}-N^{0}_{\beta\alpha})+W_{1S}(N_{\alpha\beta}-N^{0}_{\alpha\beta})+W{_2}(N_{\beta\beta}-N^{0}_{\beta\beta})-(W_{1I}+W_{1S}+W_{2})(N_{\alpha\alpha}-N^{0}_{\alpha\alpha})}

Pri formulácií tejto rovnice sme predpokladali, že pravdepodobnosti oboch jednokvantových prechodov spinu I sú veľmi podobné a možno ich považovať rovnaké (W^β_1I ≈ W^α_1I = W_1I) a že podobne zjednodušenie platí aj pre spin S (W^β_1S ≈ W^α_1S = W_1S).

Analogickým spôsobom je možno vyjadriť aj časovú zmenu populácií iných stavov:

\tiny{dN_{\alpha\beta}/dt={W_{1I}(N_{\beta\beta}-N^{0}_{\beta\beta})+W_{1S}(N_{\alpha\alpha}-N^{0}_{\alpha\alpha})+W{_0}(N_{\beta\alpha}-N^{0}_{\beta\alpha})-(W_{1I}+W_{1S}+W_{0})(N_{\alpha\beta}-N^{0}_{\alpha\beta})}}\\

\tiny{dN_{\beta\alpha}/dt=W_{1I}(N_{\alpha\alpha}-N^{0}_{\alpha\alpha})+W_{1S}(N_{\beta\beta}-N^{0}_{\beta\beta})+W{_0}(N_{\alpha\beta}-N^{0}_{\alpha\beta})-(W_{1I}+W_{1S}+W_{0})(N_{\beta\alpha}-N^{0}_{\beta\alpha})}\\

\tiny{dN_{\beta\beta}/dt=W_{1I}(N_{\alpha\beta}-N^{0}_{\alpha\beta})+W_{1S}(N_{\beta\alpha}-N^{0}_{\beta\alpha})+W{_2}(N_{\alpha\alpha}-N^{0}_{\alpha\alpha})-(W_{1I}+W_{1S}+W_{2})(N_{\beta\beta}-N^{0}_{\beta\beta})}

V každej rovnici prvé 3 členy vyjadrujú prírastok populácie daného stavu prechodom spinov z ostatných 3 stavov a posledný trojčlen naopak úbytok populácie daného stavu prechodom spinov na ostatné 3 stavy.   

Po dosadení týchto výrazov do rovníc pre dI_z/dt a dS_z/dt a následnej úprave dostaneme tzv. Solomonove rovnice, nazvané podľa autora, ktorý prvý popísal DD-relaxáciu 2 spinového systému [Solomon I. 1955. Relaxation processes in a system of two spins. Phys Rev 99:559–565.]:       

\tiny{dI_{z}/dt= -(W_{0}+2W_{1I}+W_{2})(I_{z}-I_{z}^{0})-(W_{2}-W_{0})(S_{z}-S_{z}^{0})=-R_{I}(I_{z}-I_{z}^{0})-\sigma_{IS}(S_{z}-S_{z}^{0})}\\
\tiny{dS_{z}/dt= -(W_{2}-W_{0})(I_{z}-I_{z}^{0})-(W_{0}+2W_{1S}+W_{2})(S_{z}-S_{z}^{0})=-R_{S}(S_{z}-S_{z}^{0})-\sigma_{IS}(I_{z}-I_{z}^{0})}

,kde rýchlostné konštanty R_I = (W₀ +2W_1I +W₂) a R_S = (W₀ +2W_1S +W₂) vyjadrujú vlastnú “samorelaxáciu” spinu I, resp. spinu S . Rýchlostná konštanta σ_IS = (W₂ -W₀) vyjadruje rýchlosť ich vzájomnej kros-relaxácie. Miesto rýchlostnej konštanty R sa rýchlosť samorelaxácie vyjadruje aj pomocou DD-relaxačného času T₁^DD= 1/R. Vidíme, že rýchlosť samorelaxácie i kros-relaxácie je okrem pravdepodobnosti jednokvantových prechodov (W_1I resp. W_1S ) ovplyvnená aj pravdepodobnosťami spektrálne „zakázaných“ viackvantocých prechodov (W₂ a W₀ ). Na rozdiel od kros-relaxácie však samerolaxácia existuje aj pri absencií viackvantových spektrálnych prechodov.

Integráciou diferenciálnych rovníc sú bi-exponenciálne funkcie času, priebeh ktorých okrem rýchlostných konštánt R_I, R_S  a σ_IS závisí aj od počiatočných hodnôt I_z a S_z.

Pre úplnosť popisu relaxácie je potrebné ešte odvodiť výrazy pre pravdepodobnosti jednotlivých spektrálnych prechodov. Ako bolo spomenuté vyššie odvodenie sa vykonáva na základe teórie časovo závislej poruchy Hamiltoniánu vyjadrenej pomocou H_D(t). Odvodenie je pomerné náročné a možno ho nájsť v literatúre [Gupta, A., Stait-Gardner, T., Moghaddam, M. J., Price, W. S. (2015). Dipolar relaxation revisited- A complete derivation for the two spin case. Concepts in Magnetic Resonance Part A, 44(2), 74–113. doi 10.1002/cmr.a.21334]. Na tomto mieste uvádzame iba výsledné vzťahy.

\tiny {W_{0}=\frac{1}{10}\left(\frac{\mu_{0}}{4\pi}\right)^{2} \frac{\left(\gamma_{I}\gamma_{S}  \right)^{2}}{r_{IS}^{6}}\frac{\tau_{c}}{1+\left( \omega_{I}-\omega_{S} \right)^{2}\tau^{2}_{c^{}}}=\frac{k}{r_{IS}^{6}}j\left( \omega_{I}-\omega_{S};\tau_{c} \right)}\\

\tiny {W_{2}=\frac{3}{5}\left(\frac{\mu_{0}}{4\pi}\right)^{2} \frac{\left(\gamma_{I}\gamma_{S}  \right)^{2}}{r_{IS}^{6}}\frac{\tau_{c}}{1+\left( \omega_{I}+\omega_{S} \right)^{2}\tau^{2}_{c^{}}}=\frac{6k}{r_{IS}^{6}}j\left( \omega_{I}+\omega_{S};\tau_{c} \right)}\\

\tiny {W_{1I}=\frac{3}{20}\left(\frac{\mu_{0}}{4\pi}\right)^{2} \frac{\left(\gamma_{I}\gamma_{S}  \right)^{2}}{r_{IS}^{6}}\frac{\tau_{c}}{1+ \omega_{I} ^{2}\tau^{2}_{c^{}}}=\frac{1,5k}{r_{IS}^{6}}j\left(\omega_{I};\tau_{c} \right)}\\

\tiny {W_{1S}=\frac{3}{20}\left(\frac{\mu_{0}}{4\pi}\right)^{2} \frac{\left(\gamma_{I}\gamma_{S}  \right)^{2}}{r_{IS}^{6}}\frac{\tau_{c}}{1+ \omega_{S} ^{2}\tau^{2}_{c^{}}}=\frac{1,5k}{r_{IS}^{6}}j\left(\omega_{S};\tau_{c} \right)}\\

, kde k = (μ₀γ_Iγ_S/4π)²/10 zahŕňa v sebe fyzikálne konštanty. Vidíme, že pravdepodobnosť všetkých spektrálnych prechodov pri DD relaxácií prudko klesá so vzdialenosťou medzi spinmi r_IS . Nezávisle od typu spinov sú pri r_IS > 5Å hodnoty týchto pravdepodobnosti prakticky zanedbateľné. Pravdepodobnosť jednotlivých spektrálnych prechodov (W₀ ,W_1I, W_1S a W₂) je úmerná redukovanej spektrálne hustote j(ω) pri rezonančnej frekvencií daného spektrálneho prechodu. Pre každý zo štyroch spektrálnych prechodov je to iná frekvencia (ω₀, ω_1I, ω_1S, ω₂). Parameter τ_c je korelačný čas, ktorý určuje tvar frekvenčnej distribúcie náhodných pohybov vo vzorke (pozri odsek 1.6.1 ). τ_c závisí od veľkosti molekúl a viskozity vzorky a preto aj relaxácia spinov je závislá od veľkosti molekúl a viskozity vzorky .

Rýchlostné konštanty R_I, R_S  a σ_IS možno potom vyjadriť:

\tiny{R_I=\left(W_0+2W_{1I}+W_2\right)=k/r_{IS}^6\left[j\left(\omega_I-\omega_S\right)+3j\left(\omega_I\right)+6j\left(\omega_I+\omega_S\right)\right]}\\
\tiny{R_S=\left(W_0+2W_{1S}+W_2\right)=k/r_{IS}^6\left[j\left(\omega_I-\omega_S\right)+3j\left(\omega_S\right)+6j\left(\omega_I+\omega_S\right)\right]}\\
\tiny{\sigma_{IS}=\left(W_{2\ }-\ W_0\right)=k/r_{IS}^6\left[6j\left(\omega_I+\omega_S\right)-j\left(\omega_I-\ \omega_S\right)\right]}

Ako bolo uvedené vyššie DD relaxácia má mať bi-exponenciálny charakter. Pre ¹H homonukleárny  spinový systém má však priebeh veľmi podobný mono-exponenciálnej relaxácií. Súvisí to s malými rozdielmi ¹H NMR chemických posunov, vzhľadom na veľkosť ich vzájomných DD interakcií. Z hľadiska DD-relaxácie možno preto priestorovo blízke spiny viazané v jednej molekule považovať za ekvivalentné. Takéto spiny nie je možné z hľadiska DD relaxácie rozlíšiť ale je možne pozorovať iba ich spoločnú relaxáciu. Ich ekvivalencia znamená, že pravdepodobnosti spektrálnych prechodov pre ekvivalentné spiny sú rovnaké (W_1I = W_1S => W₁ ). Pre homonukleárny 2-spinový systém potom dostaneme:

dI_z/dt + dS_z/dt = d(I_z +S_z)/dt = -(W₀ +2W₁ +W₂).[(I_z –I⁰_z)+ (S_z –S⁰_z)] – (W₂ -W₀).[ (I_z –I⁰_z)+ (S_z –S⁰_z)]
                                               = -(2W₁ +2W₂)[ (I_z + S_z)-(I⁰_z+ S⁰_z)] = 1/T₁^DD[ (I_z + S_z)-(I⁰_z+ S⁰_z)]

\tiny{dI_{z}/dt+dS_{z}/dt= d(I_z+S_z)/dt= -(W_{0}+2W_{1}+W_{2})[(I_{z}-I_{z}^{0})+(S_{z}-S_{z}^{0})]-(W_{2}-W_{0})[(I_{z}-I_{z}^{0})+(S_{z}-S_{z}^{0})]}\\
\tiny{=-(2W_{1}+2W_{2})[(I_{z}-I_{z}^{0})+(S_{z}-S_{z}^{0})]=1/T_{1}^{DD}[(I_{z}-I_{z}^{0})+(S_{z}-S_{z}^{0})]}

Po dosadení výrazov za W₁ aW₂ dostaneme pre relaxačný čas homonukleárneho systému T₁^DD=(2W₁+2W₂) vzťah:

\tiny {\frac{1}{T_1^{DD}}=\frac{3}{10}\left(\frac{\mu_0}{4\pi}\right)^2\frac{\gamma^4}{r^6}\left(\frac{\tau_c}{1+\omega^2\tau_c^2}+\frac{4\tau_c}{1+4\omega^2\tau_c^2}\right)=\frac{3k}{r^6}\left[j\left(\omega;\tau_c\right)+4j\left(2\omega;\tau_c\right)\right]}

Podobne ako DD-relaxáciu z-zložky možno odvodiť DD-relaxáciu x,y-zložiek spinov. Pri jej odvodzovaní problému je potrebné si uvedomiť, že budeme hľadať pravdepodobnosti prechodov, ktoré spôsobuje poruchový Hamiltonian  medzi vlastnými stavmi operátora I_x (alebo I_y).  Pri formulácií problému je preto výhodne stav spinov definovať v báze vlastných stavov I_x (alebo I_y) zložky spinu. Pre DD relaxačný čas T₂^DD homonukleárneho potom možno odvodiť vzťah:

\tiny{\frac{1}{T_2^{DD}}=\frac{3}{40}\left(\frac{\mu_0}{4\pi}\right)^2\frac{\gamma^4}{r^6}\left(3\tau_c+\frac{5\tau_c}{1+\omega^2\tau_c^2}+\frac{2\tau_c}{1+4\omega^2\tau_c^2}\right)=}\\ 
\tiny {=\frac{0,75k}{r^6}\left[3j\left(0;\tau_c\right)+5j\left(\omega;\tau_c\right)+2j\left(2\omega;\tau_c\right)\right]}

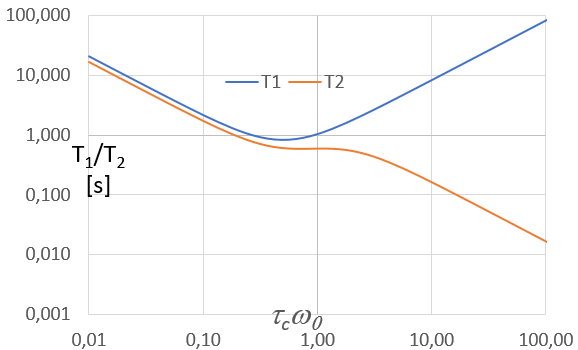
Ako vyplýva zo vyššie uvedených vzťahov oba relaxačné časy závisia od pohyblivosti molekúl (korelačného času spinov v molekule zabudovaných). Na nasledujúcom obrázku je táto závislosť ilustrovaná pre oba relaxačné časy. Vidíme, že DD-relaxácia vykazuje rovnaký trend závislosti od pohyblivosti molekúl aký bol odvodený na základe jednoduchej úvahy o efekte rôznych zložiek náhodných pohybov diskutovaný v odseku 1.6.1