Relaxácia Mz zložky magnetizácie
Podľa zákonov fenomenologickej termodynamiky je hnacou silou relaxácie nerovnovážnych systémov odchýlka ich momentálneho stavu od rovnovážneho stavu. Ako bolo ukázané vyššie, pre jednospinový I=1/2 systém je hodnota Mz zložky magnetizácie úmerná rozdielu populácie dvoch možných stavov s dobre definovanou energiou: Mz ~(Nα-Nβ). Platí to aj pre rovnovážnu magnetizáciu Mo ~ (Noα-Noβ). Pri relaxácií náhodné polia indukujú zmeny stavov spinov |α>↔|β> s pravdepodobnosťou W úmernou spektrálnej hustote náhodných pohybov J(ω) na rezonančnej frekvencií spinov. Zmeny stavov spinov pri relaxácií sa v literatúre označujú ako spektrálne prechody. Za “povolené” sa považujú tzv. jednokvantové prechody, pri ktorých sa magnetické kvantové číslo m (číslo spojené so zmenou energie systému) mení o jednotku. Treba si však uvedomiť, že pravdepodobnosť zmeny čistého stavu |α>na čistý stav |β> a naopak sa blíži k nule pretože samotný obsah čistých stavov vo vzorke je prakticky nulový. Namiesto toho sa pri relaxácií iba mení obsah stavov |α> a |β> v rôznych zmiešaných stavov (|Ψ> = cα|α> + cβ|β>), ktoré sú vo vzorke výlučne prítomné. Ako bolo spomínané vyššie zmiešané stavy sa s časom periodicky vyvíjajú s frekvenciou rovnou Larmorovej frekvencií spinov ω0. Ak náhodné polia prítomné vo vzorke majú podobnú frekvenciu, potom krátkymi náhodnými impulzami menia zloženie zmiešaného stavu (menia hodnotu koeficientov cα a cβ) tak aby ich súborovo spriemernené hodnoty <cα> a <cβ> boli v súlade s Boltzmanovym zákonom. V matematickom vyjadrení, aby (<cα>/<cβ>)2 = Noα /Noβ= e-(Eα-Eβ)/kT.
Na popis relaxácie Mz zložky magnetizácie spinov sa v literatúre využíva grafická schéma, na ktorej sú vyznačené stavy spinov s dobre definovanou energiou, ich populácie ako aj pravdepodobnosti a frekvencie spektrálnych prechodov.
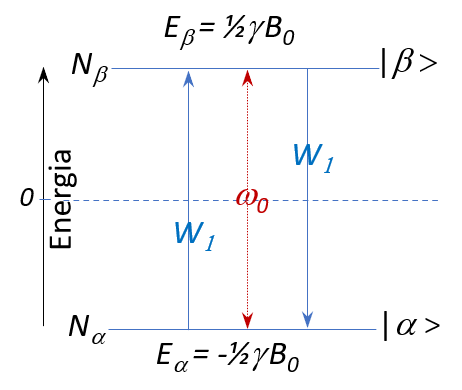
Hnacou silou zmeny Nα a Nβ je ich rozdiel od rovnovážnej hodnoty:
dNα/dt = W1(Nβ–Noβ) –W1(Nα–Noα)
dNβ/dt = W1(Nβ–Noα) –W1(Nβ–Noβ),
,kde W1 označuje pravdepodobnosť zmeny stavu spinov. W1 je pre oba smery zmeny |α>→|β> a |α>←|β> rovnaká. Pre zmenu Mz zložky magnetizácie možno potom odvodiť:
dMz/dt=(Nα-Nβ)/dt = dNα/dt-dNβ/dt
= W1(Nβ–Noβ)-W1(Nα–Noα)-W1(Nα–Noα)+W1(Nβ–Noβ)
=-2W1(Nα-Nβ) + 2W1(Noα–Noβ) = -2W1(Mz–Mo)
Dostali sme diferenciálnu rovnicu, ktorú je zvykom uvádzať v tvare:
dMz/dt =-R1(Mz–Mo ) = – (Mz–Mo )/T1
, kde (Mz–Mo) – odchýlka od rovnovážneho je hnacia sila relaxácie a R1 = 2W1 je rýchlostná konštanta relaxácie. V praxi sa rýchlosť relaxácie Mz zložky magnetizácie najčastejšie vyjadruje pomocou relaxačného času T1 = 1/R1 a nie pomocou rýchlostnej konštanty R1. Taktiež miesto „relaxácia Mz zložky“ sa často používa označenie „T1 relaxácia“.
Po integrácií možno Mz ako funkciu času vyjadriť v tvare:
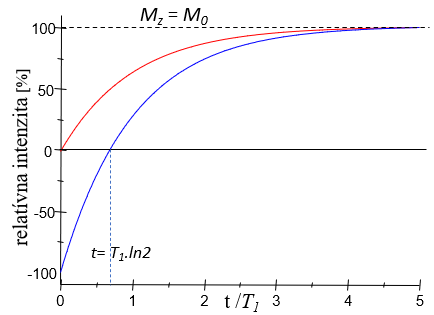
Mz(t)= Mo + (Mz(0)– Mo )( 1 – e-t/T1 ),
kde Mz(0) je počiatočná hodnota Mz(t). Ako vyplýva z časového priebehu Mz(t) (pozri nasledujúci obrázok) po čase t ≈3T1 je polarizácia vzorky obnovená na cca 90% po ľubovoľnom počiatočnom stave. Po čase t ≈ 5T1 je relaxácia Mz prakticky ukončená. Pre bežné organické vzorky je hodnota T1 v rozsahu 0,1 -10s.
Relaxácia Mxy zložky magnetizácie
Podobne ako relaxáciu z-zložky spinov možno odvodiť relaxáciu ich x,y-zložky. Pri odvodzovaní si všímame ako náhodné polia menia orientáciu a distribúciu zložiek spinu v rovine x,y. Pre tento účel je preto výhodne sledovať spektrálne prechody medzi stavmi s dobre definovanou Ixy zložkou spinu. Vektor Ixy zložky spinu s rôznou orientáciou v rovine xy (s rôznou fázou) možno formálne vyjadriť ako superpozíciu 2 nezávislých (ortogonálnych) Blochovych vektorov ľubovoľne orientovaných v rovine xy. Vyberme si 2 vektory s orientáciou v smere osi +/- x (Blochove vektory s polárnymi uhlami Θ = 90° a φ =0° , resp. Θ = 90° a φ =180°). Stav spinu spojený s týmito vektormi označme ako |αx> resp. |βx>. Stav spinu spojený s ľubovoľným vektorom orientovaným v rovine xy možno vyjadriť ako ich superpozíciu: |Ψxy> = cαx|αx> + cβx|βx>.
Ako bolo naznačené vyššie relaxácia Mxy zložky prebieha dvomi mechanizmami. Jeden súvisí s náhodnými poľami s frekvenciou na rezonancií spinov, ktoré generujú vzájomnú premenu Ix a Iy zložiek spinov nepriamo jednokvantovými spektrálnymi prechodmi cez Iz zložku spinov: Ix ↔ Iz ↔ Iy . Pravdepodobnosť týchto premien bude podobne ako v prípade relaxácie Mz zložky súvisieť s hustotou náhodných pohybov s frekvenciou blízkou rezonančnej frekvencií spinov. Označme a ju preto rovnakým symbolom W1. Druhý mechanizmus (priama zmena Ix ↔ Iy ) súvisí s náhodnými poľami orientovanými v smere osi z (Bi,z(t)) s frekvenciou blízkou nule. Pri zmene stavu |αx> ↔ |βx> sa nemení hodnota magnetického kvantového čísla m, mení sa iba fáza Ixy-zložky spinov. Tieto zmeny stavu spinov môžeme označiť ako nulkvantové spektrálne prechody a ich pravdepodobnosť symbolom Wo. V analógií s grafickou schémou popisujúcou relaxáciu Mz možno relaxáciu Mxy znázorniť schémou:
W_{1};W_{0} \\
|\alpha_x>\ \overleftrightarrow{\hspace1in}|\beta_x>\ Prechody |αx> ↔ |βx> menia hodnotu koeficientov cαx a cβx v zmiešaných stavoch |ψxy>= cαx|αx>+ cβx|βx>, čo sa prejaví zmenou orientácie (fázy) Ixy zložky spinov. Zmeny fázy sú náhodné. Ak vo vzorke existovala na začiatku nejaká usporiadanosť fázy (fázová koherencia) Ixy zložiek spinov, postupom času sa jej usporiadanosť bude zmenšovať. Z termodynamického hľadiska rast neusporiadanosti znamená rast entropie systému. Rovnováha (maximálna hodnota entropie) sa dosiahne ak sú všetky orientácie Blochovho vektora |ψx> v rovine xy rovnako pravdepodobne, čiže ak Mxy = 0, resp. ak súborovo spriemernené koeficienty vyjadrujúce obsah stavov |αx> a |βx> v zmiešanom stave |ψxy> majú rovnakú hodnotu <c2αx>= <c2βx>.
Podobne ako pre Mz zložku magnetizácie aj pre jej Mxy zložku možno časový priebeh relaxácie formulovať pomocou analogickej lineárnej fenomenologickej diferenciálnej rovnice 1.stupňa, kde hnacou silou relaxácie je rozdiel od rovnovážneho stavu. Oproti relaxácií Mz zložky je rozdielny rovnovážny stav (Moxy = 0 ). Rozdielne sú aj konštanty charakterizujúce rýchlosť relaxácie: rýchlostná konštanta R2 a teda aj relaxačný čas T2=1/R2.
dMxy/dt =-R2(Mxy-Moxy) = –(Mxy– 0 )/T2= -Mxy/T2
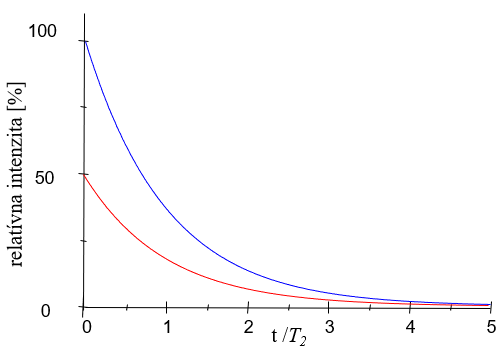
Po integrácií možno Mxy ako funkciu času vyjadriť v tvare: Mxy(t)= Mxy (0).e-t/T2
Ako vyplýva z časového priebehu Mxy(t) (pozri nasledujúci obrázok) po čase t ≈3-5T2 je relaxácia Mxy prakticky ukončená.
Ako bolo spomenuté vyššie zánik fázovej koherencie podporuje aj nehomogenita poľa Bo. V nehomogénnom poli je preto výsledná rýchlosť zániku Mxy zložky magnetizácie zvýšená o príspevok úmerný nehomogenite poľa ∆Bo :
R2*= 1/T2*= R2 +γ∆Bo = 1/T2+γ∆Bo
,kde R2*a T2* charakterizujú T2 relaxáciu v nehomogénnom magnetickom poli, ∆Bo vyjadruje priemernú hodnotu nehomogenít Bo a γ je gyromagnetický pomer meraného spinu.
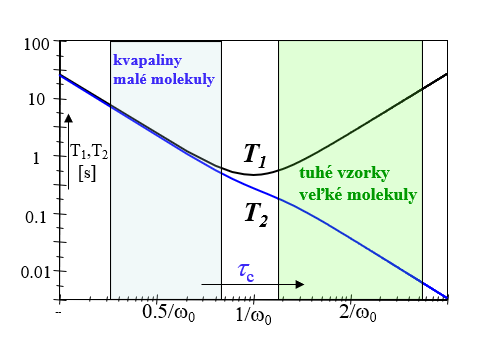
Relaxačné časy a ich závislosť od pohyblivosti molekúl.
Na presné určovanie relaxačných časov T1 a T2 boli navrhnuté špeciálne NMR experimenty (pozri v ďalšom). Z praxe vieme, že relaxačné časy T1 a T2 bežných molekúl sú v rozmedzí 10-3 až 102 s. Z diskusie v predchádzajúcom odseku vieme že rozdiely v rýchlosti relaxácie podobných s
Na rozdiel od relaxácie Mz zložky magnetizácie k relaxácií jej Mxy zložky prispievajú okrem náhodných poli na rezonančnej frekvencií aj náhodné polia z oblasti veľmi malých frekvencií. Pre malé organické molekuly (τc < 1/ωo) je však tento príspevok malý a preto hodnota T2 je pre tieto molekuly podobná hodnote T1 a je obvykle v rozsahu 0,01 -10s. Pre veľké molekuly (τc > 1/ωo) je však tento príspevok významný, a pre tieto molekuly platí T2 < T1. Závislosť T2 od pohyblivosti molekúl je na rozdiel od T1 monotónne klesajúca s veľkosťou molekúl.